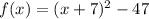Answer:
The new function is
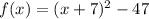 .
.
Explanation:
The given function is
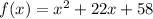
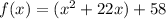
To find the vertex from add and subtract
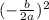 in the parenthesis.
in the parenthesis.
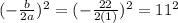
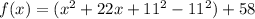
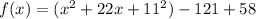
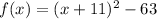
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/2018/formulas/mathematics/high-school/bo5iuom7ylypazgw1zsgqujjt1wmu3vonv.png)
The vertex of the given function is (-11,-63).
It is given that the function f(x) is translated 4 units to the right and 16 units up.
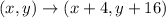
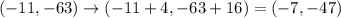
The vertex of new function is (-7.-47). So the new function is