Question

Suppose you want to decrease your margin of error by a factor of 3. by what factor, do you need to increase your sample size? in other words, if you want to decrease your margin of error from 12% to 4% by what factor do you need to increase your sample size?

Answer 1

The sample size, n required to produce a margin of error, M, in a probability proportion distribution is given by:


`n= (p(1-p)z_(\alpha/2)^2)/(M^2)`

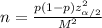
The above formular shows that the sample size is inversely proportional to the Margin of error.

Then we have:


`n= (k)/(M^2)`

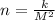
where k is some constant.

Now suppose we decrease M by a factor of 3,


`\left(i.e.\ (M_1)/(M_2) =3\right)`


`n_1= (k)/(M_1^2) \\ \\ n_2= (k)/(M_2^2) \\ \\ (n_2)/(n_1) = (k)/(M_2^2) / (k)/(M_1^2) = (k)/(M_2^2) * (M_1^2)/(k) = (M_1^2)/(M^2_2) =\left( (M_1)/(M_2) \right)^2=3^2=9 \\ \\ n_2=9n_1`

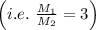
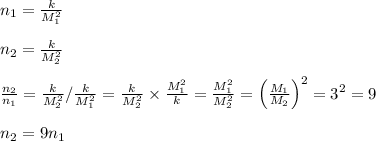
Therefore, if we decrease the Margin of error by a factor of 3, we need to increase the sample size by a factor of 9.