Question

Use completing the square to solve for x in the equation (x+7)(x-9)=25

x = –4 or 6
x = –2 or 14
x = 1 ± sqrt(89)
x = 1 ± sqrt(87)

Answer 1

First, we need to expand the left hand side expression:


`(x+7)(x-9)=x^2-9x+7x-63=x^2-2x-63.`

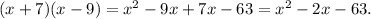
The quadratic and linear terms
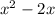
`x^2-2x` are 'produced' from the expansion of the binomial
`(x-1)^2` which is
`x^2-2x+1`.


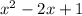
Thus, we can write
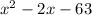
`x^2-2x-63` as
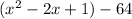
`(x^2-2x+1)-64`, which is equal to

`(x-1)^2-64.`


Thus, the equation is
`(x-1)^2-64=25`. Adding 64 to both sides, we have:

`(x-1)^2=89`.

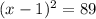
This means that x-1 is either
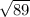
`√(89)` or
`-√(89)`.

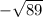
Finally, we see that x is either
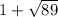
`1+ √(89)` or
`1 -√(89)`.


Answer: x = 1 ± sqrt(89)