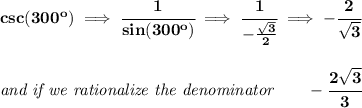Question

Find the exact value of csc(-1860).

Not exactly for sure where to start, i've gotten to this,

csc(300)=csc(360-60)=csc(-60)

but I am not for sure where to go after, help would be appreciated.

Answer 1

now, there are 360° in a circle, how many times does 360° go into 1860°?

well, let's check that,
`\bf \cfrac{1860}{360}\implies \cfrac{31}{6}\implies 5(1)/(6)\implies 5+(1)/(6)`

now, this is a negative angle, so it's going clockwise, like a clock moves, so it goes around the circle clockwise 5 times fully, and then it goes 1/6 extra.

well, we know 360° is in a circle, how many degrees in 1/6 of 360°? well, is just 360/6 or their product, and that's just 60°.

so -1860, is an angle that goes clockwise, negative, 5 times fully, then goes an extra 60° passed.

5 times fully will land you back at the 0 location, if you move further down 60° clockwise, that'll land you on the IV quadrant, with an angle of -60°.

therefore, the csc(-1860°) is the same as the angle of csc(-60°), which is the same as the csc(360° - 60°) or csc(300°).


`\bf csc(300^o)\implies \cfrac{1}{sin(300^o)}\implies \cfrac{1}{-(√(3))/(2)}\implies -\cfrac{2}{√(3)} \\\\\\ \textit{and if we rationalize the denominator}\qquad -\cfrac{2√(3)}{3}`