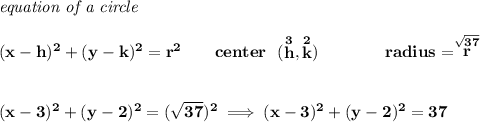so, we know the circle is at (3, 2), and we also know that a point on the circle is at 9,3, well, what is the distance from the center of the circle to any point on the circle? well is just the radius.
Therefore the distance between those two points is the radius, let's check what that is,
![\bf ~~~~~~~~~~~~\textit{distance between 2 points}\\ \quad \\ \begin{array}{ccccccccc} &&x_1&&y_1&&x_2&&y_2\\ % (a,b) &&(~{{ 3}} &,&{{ 2}}~) % (c,d) &&(~{{ 9}} &,&{{ 3}}~) \end{array}\qquad % distance value d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2} \\\\\\ d=√((9-3)^2+(3-2)^2)\implies d=√(6^2+1^2)\implies d=√(37)]()
now, what is the equation of a circle whose center is at 3,2 and has a radius of √(37)?