Answer:
P = 510 Ns
Step-by-step explanation:
Momentum is defined as the quantity of motion contained in a body. Mathematically momentum is defined as the product of mass and the velocity of the body. So in order to find out the momentum of the referee after the collision with the football player, we can use the following formula:

where,
P = Momentum of the referee after the collision = ?
m = mass of the referee = 85 kg
v = speed of the referee after collision = 6 m/s
Therefore,
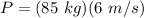
P = 510 Ns