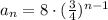Answer:
The explicit rule for this sequence is;
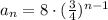
Explanation:
Given the statement: A recursive rule for a geometric sequence is
 and
and
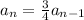
for n= 2;
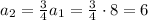
Similarly for n = 3;
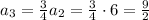
Therefore, we get a geometric sequence i.e,

Now, to find the explicit rule for this geometric sequence:
A geometric sequence states that a sequence of numbers that follows a pattern were the next term is found by multiplying by a constant called the common ratio(r).
It is given by:
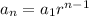 where
where
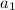 is the first term, r s the common ratio and n is the number of terms;
is the first term, r s the common ratio and n is the number of terms;
In the given sequence:
 ,
,
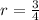
then, the explicit rule for this sequence is;