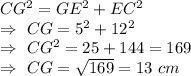Question

DG, EG, and FG are perpendicular bisectors of the sides of △ ABC . DG=5 centimeters and BD=12 centimeters.

What is CG ?

Enter your answer in the box.

Answer 1

Hiya! The answer is 13. Trust me, I had this exact same question!

CG is 13 cm

Answer 2

Answer:- CG= 13 cm

Explanation:-

Given : Δ ABC where DG, EG, and FG are perpendicular bisectors of the sides intersecting at point G .

⇒ G is the circumcenter of the triangle.

⇒BG, CG and AG are the angle bisectors of the triangle.

Now, from the given figure

In ΔBDG and ΔBEG

∠D = ∠ E [right angle]

BG=BG [reflexive property]

∠DBG=∠EBG [Definition of angle bisector]

⇒ΔBDG ≅ ΔBEG [AAS congruence theorem]

Thus BD=BE= 12 cm [CPCT]

DG=EG= 5 cm [CPCT] .....(1)

Now In ΔBGE and ΔCGE

GE=GE [reflexive property]

∠BEG=∠CEG [right angle]

BE=EC [Definition of perpendicular bisector]

⇒ΔBGE ≅ ΔCGE [SAS postulate]

⇒BE=CE=12 cm ......(from (1))

and GE= 5 cm

As ΔCGE is right angle then by Pythagoras theorem,

`CG^2=GE^2+EC^2\\\Rightarrow\ CG=5^2+12^2\\\Rightarrow\ CG^2=25+144=169\\\Rightarrow\ CG=√(169)=13\ cm`