Question

Calculate the average rate of change of the function y= ½x² - 1 over the interval -2 ≤ x ≤ 0​

Answer 1

Answer: The average rate of change of the function in that interval is r = -1

Explanation:

When we have a function f(x), the average rate of change in an interval:

a ≤ x ≤ b

Is calculated as:

`rate = (f(b) - f(a))/(b - a)`

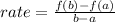
In this case, the function is:

y = f(x) = (1/2)*x^2 - 1

And the interval is:

-2 ≤ x ≤ 0​

Then the rate of change will be:

`rate = (f(0) - f(-2))/(0 -(-2)) = (((1/2)*(0)^2 - 1) -((1/2)(-2)^2 - 1))/(2) = (-2)/(2) = -1`

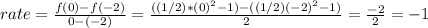
The average rate of change of that function in that interval is r = -1