Question

This set of points is on the graph of a function.

{(−3, 9), (−1, 1), (0, 0), (2, 4)}

Which points are on the graph of the inverse?

Select each correct answer.



(0, 0)

(1, −1)

(−9, 3)

(4, 2)
What is the inverse of f(x)=−3x+5 ?



f−1(x)=13x−53

f−1(x)=3x−5

f−1(x)=−3x+5

f−1(x)=−13x+53

Answer 1

1. (0, 0)
2. f(x) = −3x+5
f(x) = y, switch the x and y
x = -3y+5, now solve for y:
-3y +5-5 = x-5
-3y = x-5
-3y/-3 = (x-5)/-3
y = -x/3 + 5/3
Dunno why that's not an option

Answer 2

1. (0, 0), (1, −1) and (4, 2)

2. The correct option is 4.

Explanation:

1.

The given function is

{(−3, 9), (−1, 1), (0, 0), (2, 4)}

If a function is defined as

`f=\{(x,y):x\in R, y\in R\}`

then the inverse of the function is

`f^(-1)=\{(y,x):x\in R, y\in R\}`

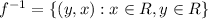
The inverse of the given function is

{(9,−3), (1,−1), (0, 0), (4,2)}

Therefore the points (0, 0), (1, −1) and (4, 2) are on the graph of the inverse.

2.

The given function is

`f(x)=-3x+5`

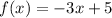
The equation of the function is

`y=-3x+5`

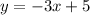
Interchange x and y.

`x=-3y+5`

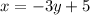
Isolate y.

`x-5=-3y`

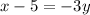
Divide both sides by -3.

`(x-5)/(-3)=y`

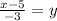
The inverse of the given function is

`f^(-1)(x)=-(x)/(3)+(5)/(3)`

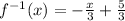
Therefore the correct option is 4.