Given that S6 is 133 and the common ratio (r) is -2/3.
We know that the sum of n terms of a gp whose common ratio is less than 1 is
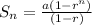
So,
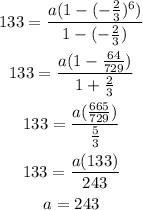
Now, we have known that the first term of the gp is 243.
So, the second term is:
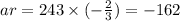
The third term is:
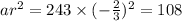
Thus, the first three terms are 243, -162, 108.