Question

A worker was paid a salary of $10,500 in 1985. Each year, a salary increase of 6% of the previous year's salary was awarded. How much did the worker earn from the beginning of 1985 through the end of 2010?

A $45,064.64
B $256,527.63
C $576,077.38
D $621,142.02

Answer 1

Note that 6% converted to a decimal number is 6/100=0.06. Also note that 6% of a certain quantity x is 0.06x.

Here is how much the worker earned each year:


In the year 1985 the worker earned $10,500.

In the year 1986 the worker earned $10,500 + 0.06($10,500). Factorizing $10,500, we can write this sum as:

$10,500(1+0.06).



In the year 1987 the worker earned

$10,500(1+0.06) + 0.06[$10,500(1+0.06)].

Now we can factorize $10,500(1+0.06) and write the earnings as:

$10,500(1+0.06) [1+0.06]=
`$10,500(1.06)^2`.


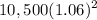Similarly we can check that in the year 1987 the worker earned
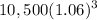`$10,500(1.06)^3`, which makes the pattern clear.


We can count that from the year 1985 to 1987 we had 2+1 salaries, so from 1985 to 2010 there are 2010-1985+1=26 salaries. This means that the total paid salaries are:


`10,500+10,500(1.06)^1+10,500(1.06)^2+10,500(1.06)^3...10,500(1.06)^(26)`.

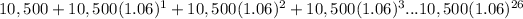Factorizing, we have


`=10,500[1+1.06+(1.06)^2+(1.06)^3+...+(1.06)^(26)]=10,500\cdot[1+1.06+(1.06)^2+(1.06)^3+...+(1.06)^(26)]`

We recognize the sum as the geometric sum with first term 1 and common ratio 1.06, applying the formula


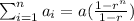`\sum_(i=1)^(n) a_i= a((1-r^n)/(1-r))` (where a is the first term and r is the common ratio) we have:


`\sum_(i=1)^(26) a_i= 1((1-(1.06)^(26))/(1-1.06))= (1-4.55)/(-0.06)= 59.17`.



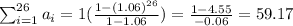Finally, multiplying 10,500 by 59.17 we have 621.285 ($).


The answer we found is very close to D. The difference can be explained by the accuracy of the values used in calculation, most important, in calculating
`(1.06)^(26)`.


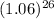Answer: D