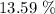Question

a. A population of values has a normal distribution with μ =153 and σ = 39.5You intend to draw a random sample of size n = 196Find P2, which is the score separating the bottom 2% scores from the top 98% scores. P2 (for single values) = Find P2, which is the mean separating the bottom 2% means from the top 98% means. P2 (for sample means) = Enter your answers as numbers accurate to 1 decimal place.round your answer to ONE digit after the decimal point!Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.b. A company has a policy of retiring company cars; this policy looks at number of miles driven, purpose of trips, style of car and other features. The distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 45 months and a standard deviation of 3 months. Using the empirical rule (as presented in the book), what is the approximate percentage of cars that remain in service between 48 and 51 months?

Answer 1

For the part B

we have the following information

To get the approximate percentage that remains in service between 48 and 51 months, we will use the formula

and then follow the steps below

Step 1.

We will find the z-score corresponding to both 48 and 51 months

For 48 months

`\begin{gathered} z=(48-45)/(3) \\ z=(3)/(3)=1 \end{gathered}`

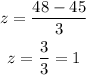
for 51 months

`z=(51-45)/(3)=(6)/(3)=2`

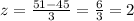
The plot of the distribution is given below

From the plot above, we can observe that the probability is

`0.1359`

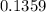
In terms of percentage, the value is

`\begin{gathered} 0.1359*100percent\text{ } \\ = \\ 0.1359*100\text{ \%} \end{gathered}`

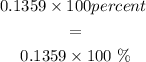
Thus, we will have

`13.59\text{ \%}`