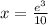Question

Please help me solve ln 5 +ln 2x=3

Answer 1

`x=(e^3)/(10)`

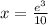
Explanation:

We have the equation

`ln5 +ln 2x=3`

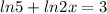
The first step to simplify is to use the following property of logarithms

`lna+lnb=ln(a*b)`, in this case a=5 and b=2x

So the original equation becomes:

`ln(5*2x)=3`

`ln(10x)=3`

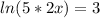
The inverse operation of the natural logarithm is the exponential
`e`

Thus Using the following property:

`e^(lnk) =k`

The equation now is:

`e^(ln10x) =e^(3)`

⇒
`10x=e^3`

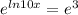
thus, x will be:

`x=(e^3)/(10)`

Answer 2

ln(5) + ln(2x) = 3 Remember that ln(a) + ln(b) = ln(ab)
ln(10x) = 3
This statement means that the power we have to raise e to in order to get 10x is 3. Therefor:
e³ = 10x
x = e³/10