Question

√4x-3=2x-3 can you compute it?

Answer 1

Given the equation:

`\sqrt[]{4x-3}=2x-3`

Let's solve the equation for x.

Square both sides:

`\begin{gathered} (\sqrt[]{4x-3})^2=(2x-3)^2 \\ \\ 4x-3=(2x-3)(2x-3) \end{gathered}`

Solving further:

Expand using the FOIL method.

`4x-3=2x(2x-3)-3(2x-3)`

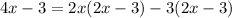
Apply distributigve property:

`\begin{gathered} 4x-3=2x(2x)+2x(-3)-3(2x)-3(-3) \\ \\ 4x-3=4x^2-6x-6x+9 \\ \\ 4x-3=4x^2-12x+9 \end{gathered}`

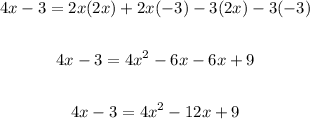
Move all terms to the left and equate to zero:

`\begin{gathered} 4x^2-12x+9-4x+3=0 \\ \\ 4x^2-12x-4x+9+3=0 \\ \\ 4x^2-16x+12=0 \end{gathered}`

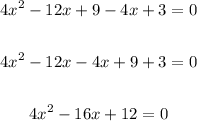
Factor the left side of the equation:

`\begin{gathered} 4(x^2-4x+3)=0 \\ \\ 4(x-3)(x-1)=0 \end{gathered}`

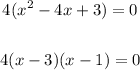
Equate each factor to zero and solve for x.

x - 3 = 0

Add 3 to both sides:

x - 3 + 3 = 0 + 3

x = 3

x - 1 = 0

Add 1 to both sides:

x - 1 + 1 = 0 + 1

x = 1

Hence, we have:

x = 3 and 1

Now, let's exclude the solution that do not make the equation true.

Input 3 for x in the equation:

`\begin{gathered} \sqrt[]{4(3)-3}=2(3)-3 \\ \\ \sqrt[]{12-3}=6-3 \\ \\ \sqrt[]{9}=3 \\ \\ 3=3 \end{gathered}`

The value of 3 makes the equation true.

Input 1 for x in the equation and evaluate:

`\begin{gathered} \sqrt[]{4(1)-3}=2(1)-3 \\ \\ \sqrt[]{1}=-1 \\ \\ 1\\e-1 \end{gathered}`

The value of 1 do NOT make the equation true.

Therefore, the correct solution for x in the equation is 3.

ANSWER:

x = 3