Given the equation:
![\sqrt[]{4x-3}=2x-3](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/23ddqera0dormvuqck26.png)
Let's solve the equation for x.
Square both sides:
![\begin{gathered} (\sqrt[]{4x-3})^2=(2x-3)^2 \\ \\ 4x-3=(2x-3)(2x-3) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/3w7hm3il83v6at81jdst.png)
Solving further:
Expand using the FOIL method.

Apply distributigve property:
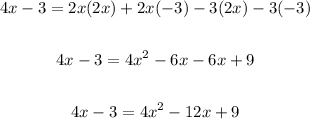
Move all terms to the left and equate to zero:
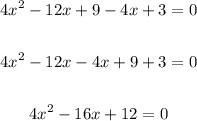
Factor the left side of the equation:

Equate each factor to zero and solve for x.
x - 3 = 0
Add 3 to both sides:
x - 3 + 3 = 0 + 3
x = 3
x - 1 = 0
Add 1 to both sides:
x - 1 + 1 = 0 + 1
x = 1
Hence, we have:
x = 3 and 1
Now, let's exclude the solution that do not make the equation true.
Input 3 for x in the equation:
![\begin{gathered} \sqrt[]{4(3)-3}=2(3)-3 \\ \\ \sqrt[]{12-3}=6-3 \\ \\ \sqrt[]{9}=3 \\ \\ 3=3 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/grzogyayenxvzwqen6ua.png)
The value of 3 makes the equation true.
Input 1 for x in the equation and evaluate:
![\begin{gathered} \sqrt[]{4(1)-3}=2(1)-3 \\ \\ \sqrt[]{1}=-1 \\ \\ 1\\e-1 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/r60jnx22o9n2hadgywih.png)
The value of 1 do NOT make the equation true.
Therefore, the correct solution for x in the equation is 3.
ANSWER:
x = 3