To find the area of the shaded region:
1. Find the area of the semicircle:
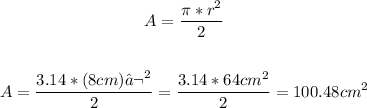
2. Find the area of the triangle:
the base of the triangle is the diameter of the semicircle (twice the radius)
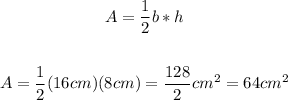
3. Subtract the area of the triangle from the area of the semicirle:
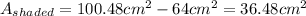
Then, the area of the shaded region is 36.48 square centimeters