Question

he volume of the pyramid shown in the figure is cubic centimeters. If the slant height of the pyramid increases by 4 centimeters and its height increases by 2 centimeters, the volume of the pyramid increases by cubic centimeters.

Answer 1

218 hope this helped :)

Answer 2

Part a) The volume of the original pyramid is
`15\ cm^(3)`

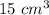
Part b) The volume of the pyramid increases by
`6\ cm^(3)`

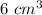
Explanation:

we know that

The volume of the pyramid is equal to

`V=(1)/(3)Bh`

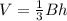
where

B is the area of the base

h is the height of pyramid

see the attached figure to better understand the problem

Step 1

Find the volume of the original pyramid

the area of the base B is equal to

`B=3^(2)=9\ cm^(2)`

`h=5\ cm`

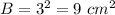
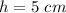
substitute

`V=(1)/(3)(9)(5)=15\ cm^(3)`

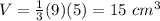
Step 2

Find the volume of the new pyramid

`B=9\ cm^(2)` -------> the area of the base is the same

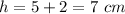`h=5+2=7\ cm` ------> the height increase by
`2\ cm`

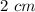
substitute

`V=(1)/(3)(9)(7)=21\ cm^(3)`

Subtract the original volume from the new volume

`21\ cm^(3)-15\ cm^(3)=6\ cm^(3)`