The equation for the n-th term of the geometric sequence is
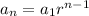
where
a₁ = the first term
r = the common ratio.
a₄ = 6, therefore
a₁ r³ = 6 (1)
a₉ = -192, therefore
a₁ r⁸ = -192 (2)
Divide equation (2) by equation (1).
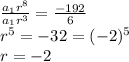
From (1), obtain
a₁(-2)³ = 6
-8a₁ = 6
a₁ = -3/4
Answer: -3/4