Question

What are the solutions of the equation x^4 - 5x^2 - 14 = 0? Use factoring to solve

A) x = +-√7 and x = +-√2

B) x = +-i√7 and x = +-i√2

C) x = +-i√7 and x = +-√2

D) x = +-√7 and x = +-i√2

Answer 1

It factorises to (x^2 +2)(x^2 -7)
This makes the roots d

Answer 2

D) x = +-√7 and x = +-i√2

Explanation:

Given:

x^4 -5x^2 -14 = 0

This can be written as

x^4 + 2x^2 - 7x^2 -14 = 0

x^2(x^2 + 2) -7(x^2 + 2) = 0

(x^2 +2)(x^2 - 7) = 0

x^2 + 2 = 0 and x^2 - 7 = 0

x^2 = -2

x =
`√(-2)`

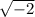
x = ±i√2

x^2 - 7 = 0

x^2 = 7

x = ±√7

Therefore, solutions are D) x = +-√7 and x = +-i√2

Hope this will helpful.

Thank you.