Answer:
The correct option is 2.
Explanation:
From the given graph it is noticed that the related line passing through the points (0,-2) and (1,0).
If a line passing through two points, then the equation of line is
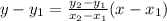
The related equation is
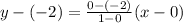
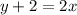
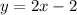
So, the related equation is
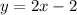 .
.
From the graph it is noticed that the point (0,0) contained in the shaded region.
check the related equation by (0,0).

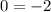
This statement is true if the sign is
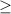 insted of equality.
insted of equality.
Therefore the required inequality is
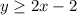
Option 2 is correct.