Answer
The slope of the line is -8
Explanation
To find the slope of our line we are going to use the slope formula:
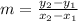
where
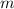 is the slope of the line
is the slope of the line
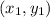 are coordinates of the first point
are coordinates of the first point
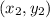 are the coordinates of the second point
are the coordinates of the second point
We know that the first point on our graph is (0, 6), so
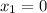 and
and
 . We also know that the second point is (1, -2), so
. We also know that the second point is (1, -2), so
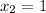 and
and
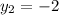 . Let's replace those values in our formula:
. Let's replace those values in our formula:
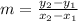
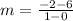
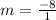
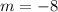
We can conclude that the slope of the line passing through the points (0, 6) and (1, -2) is -8.