Question

Find the dimensions of a rectangle with perimeter 60 m whose area is as large as possible. (if both values are the same number, enter it into both blanks.)

Answer 1

I am just doing this because I am niceyeah lol

Answer 2

Answer: Area of rectangle = 225 square meter.

Step-by-step explanation:

Since we have given that

Perimeter of rectangle = 60 m

Since we have also state that both the value of dimensions are equal to each other ,

Length = breadth

As we know the formula of perimeter of rectangle which is given as

`2(Length+Breadth)=60\\\\Length+Breadth=(60)/(2)=30\\\\Length=Breadth=15\ m`

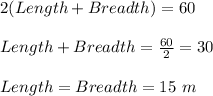
So, Area of rectangle is as large as possible is given as

`Length* breadth=15* 15=225\ m^2`

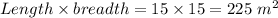
Hence, area of rectangle = 225 square meter.