Question

An open box is to be made from a rectangular piece of cardboard which is 20 inches by 28 inches by cutting equal squares from the corners and turning up the sides. find the size of the square which gives the box of largest volume.

Answer 1

Let the side length of the squares that are cut out from the corners be x, then the length of the base of the open box formed is 28 - 2x while the width of the box is 20 - 2x and the height is x.

The volume of a rectangular box is given by length x width x height

Thus,


`Volume = x(28 - 2x)(20 - 2x) \\ \\ =x(560 - 96x + 4x^2)=4x^3-96x^2+560x`

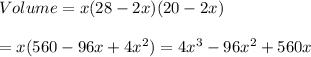
For maximum volume, the differentiation of the volume with respect to x is 0 and the second derivative test yeilds a negative number,

Thus


`(dV)/(dx) =0 \\ \\ \Rightarrow12x^2-192x+560=0 \\ \\ \Rightarrow x\approx12.16\ or\ x\approx3.84`


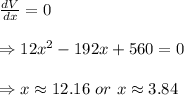
`\left. (d^2V)/(dx^2) \right|_(x=12.16)=[24x-192]_(x=12.16) \\ \\ =24(12.16)-192=291.84-192 \\ \\ =99.84 \\ \\ \left. (d^2V)/(dx^2) \right|_(x=3.84)=[24x-192]_(x=3.84) \\ \\ =24(3.84)-192=92.16-192 \\ \\ =-99.84`

Since the second derivative is negative when x = 3.84, thus the value x and hence the size of the square which gives the box of largest volume is 3.84 inches.