Question

Calculate the work (w) and δeo, in kj, at 298 k and 1 atm pressure, for the combustion of one mole of c6h6 (g). first write and balance the equation. the products will be co2 (g) and h2o (g). the value of δho for this reaction is -3169.3 kj/mol.

Answer 1

The enthalpy change for the combustion of one mole of benzene (C6H6) is -3169.3 kJ, which is also the work done under constant pressure. The electromotive force (Δeo) is not provided and cannot be calculated with the given information.

Step-by-step explanation:

To calculate the work (w) and Δeo for the combustion of one mole of C6H6 (g), we first must write and balance the chemical equation:

2C6H6(g) + 15O2(g) → 12CO2(g) + 6H2O(l)

ΔHo for this reaction is -3169.3 kJ/mol, we can say that the heat released (enthalpy change) for the combustion of one mole of C6H6 is -3169.3 kJ. Assuming that the reaction is carried out under constant pressure, the enthalpy change can also represent the work done.

The value of Δeo is the standard electromotive force, which is not directly given in this problem and requires additional information like the standard reduction potentials to calculate.

Answer 2

Answer : The value of w and ΔE is, 1.24 kJ and -3170.5 kJ/mol respectively.

Explanation :

Formula used :

`\Delta H=\Delta E+\Delta n_gRT`

`\Delta H` = change in enthalpy = -3169.3 kJ/mol = -3169300 J/mol

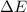`\Delta E` = change in internal energy

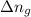`\Delta n_g` = change in moles

R = gas constant = 8.314 J/mol.K

T = temperature = 298 K

The balanced chemical reaction will be:

`C_2H_6(g)+(7)/(2)O_2(g)\rightarrow 2CO_2(g)+3H_2O(g)`

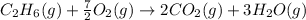
In this case:

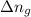`\Delta n_g` = change in moles

Change in moles = Number of moles of product side - Number of moles of reactant side

According to the reaction:

Change in moles = [3+2] - [1+ (7/2)]= 0.5 mole

`\Delta H=\Delta E+\Delta n_gRT`

`-3169300J/mol=\Delta E+(0.5mol)* (8.314J/mol.K)* (298K)`

`\Delta E=-3170.5kJ/mol`

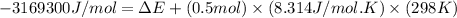
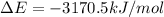
Now we have to calculate the work done.

`w=p\Delta V=\Delta nRT`

`w=(0.5mol)* (8.314J/mol.K)* (298K)`

`w=1.24kJ`

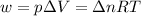
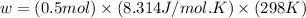
Therefore, the value of w and ΔE is, 1.24 kJ and -3170.5 kJ/mol respectively.