Question

What are the x- and y- coordinates of point E, which partitions the directed line segment from J to K into a ratio of 1:4? (–13, –3) (–7, –1) (–5, 0) (17, 11)

Answer 1

(-7,-1)

Step-by-step explanation:

Given that the point J has coordinates as (-15,-5) and K has coordinates as

(25,15)

E divides the line segment JK in the ratio 1:4 internally

Here the ratio is m:n where m =1 and n =4

The formula for a point dividing the line joining (x1,y1) and (x2,y2) in the ratio m:n is

`((mx_2 +nx_1)/(m+n), (my_2 +ny_1)/(m+n))`

Substitute for m,n and also other points

WE get

Coordinate of E=

`((1(25)+4(-15))/(1+4),(1(15)+4(-5))/(1+4)) \\=(-7, -1)`

Answer 2

I added a screenshot of the complete question.

Answer:

(-7, -1)

Step-by-step explanation:

The formulas given to calculated the x and y coordinates are as follows:

`x = ((m)/(m+n))(x_(2)-x_(1)) + x_(1)\\\\y = ((m)/(m+n))(y_(2)-y_(1)) + y_(1)`

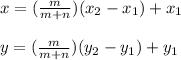
Let's define the variables used:

(x₁ , y₁) are the coordinates of the first point while (x₂ , y₂) are the coordinates of the second point.

We are given that the segment is directed from J to K, therefore:

First point is J ..........> (x₁ , y₁) is (-15, -5)

Second point is K ....> (x₂ , y₂) is (25, 15)

m and n defined the portion of the partitioned segment (JE : EK). It is given that this ratio is 1:4. Therefore:

m = 1 and n = 4

Finally, let's substitute with these variables in the equations as follows:

`x = ((1)/(1+4))(25-(-15)) + (-15) = -7\\\\y = ((1)/(1+4))(15-(-5)) + (-5) = -1`

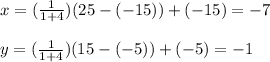
Based on the above, the coordinates of point E are (-7, -1)

Hope this helps :)