Question

A 7.0-kilogram cart, A, and a 3.0-kilogram cart, B, are initially held together at rest on a horizontal, frictionless surface. When a compressed spring attached to one of the carts is released, the carts are pushed apart. After the spring is released, the speed of cart B is 6.0 meters per second, as represented in the diagram belowWhat is the speed of cart A after the spring is released?

Answer 1

The speed of cart A after the spring is released is 2.57 m/s.

Given the following data:

• Mass of cart A = 7.0 kg

• Initial velocity of cart A and B = 0 m/s (since they were held at rest).

• Mass of cart B = 3.0 kg

• Final velocity of cart B = 6.0 m/s

To find the speed of cart A after the spring is released, we would apply the law of conservation of momentum:

`M_AV_A - M_BV_B = M_AV_(fA) + M_BV_(fB)`

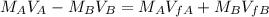
Where:

• 
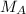  `M_A` is the mass of the first cart.

• 
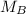  `M_B` is the mass of the second cart.

• 
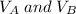  `V_A \;and\; V_B` are the initial velocities.

• 
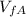  `V_(fA)` is the initial velocity of the first cart.

• 
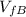  `V_(fB)` is the final velocity of the second cart.

Substituting the given parameters into the formula, we have;

`7 * 0 - 3 * 0 = 7 * -V_(fA) + 3 * 6\\\\0 = -7V_(fA) + 18\\\\V_(fA) = (18)/(7)\\\\V_(fA) = 2.57 m/s`

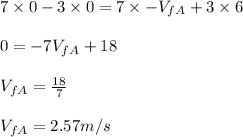
Note: The negative sign indicate that cart A is moving to the left direction.

Answer 2

For this problem, we use the conservation of momentum as a solution. Since momentum is mass times velocity, then,

m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'
where
v₁ and v₂ are initial velocities of cart A and B, respectively
v₁' and v₂' are final velocities of cart A and B, respectively
m₁ and m₂ are masses of cart A and B, respectively

(7 kg)(0 m/s) + (3 kg)(0 m/s) = (7 kg)(v₁') + (3 kg)(6 m/s)
Solving for v₁',
v₁' = -2.57 m/s

Therefore, the speed of cart A is at 2.57 m/s at the direction opposite of cart B.