Answer:
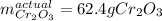
Step-by-step explanation:
Hello!
In this case, according to the reaction:
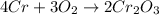
We can see there is a 4:2 mole ratio between chromium and chromium (III) oxide, this, for the given 56.2 g of chromium, the theoretical yield of the oxide product is computed down below:
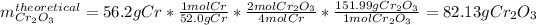
Now, considering the 76.0-% yield for this reaction, the actual yield turns out:
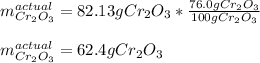
Best regards!