Answer:
The volume of the container is:
2880 cm^3
Explanation:
In order to find the volume of the container we need to find the volume of the cylinder and volume of two half spheres.
i.e.
Volume of container=Volume of cylinder+Volume of two half spheres.
We know that the volume of cylinder is given by:
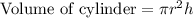
where h is the height of the cylinder and r denote the radius of the cylinder.
Also, volume of 1 half sphere is given by:
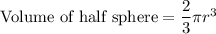
where r is the radius of half sphere.
Hence, Volume of 2 half spheres is:

Hence,
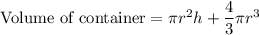
From the given information in the question we have:
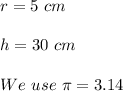
Hence, by putting these values in the expression (1) and solving we get:
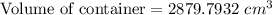
which on rounding off gives:
2880 cm^3