Answer:

Explanation:
The given expression is
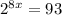
To solve this we have to apply logarithms as follows
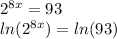
Now, applying properties of logarithms, we have
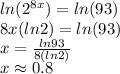
Therefore, the answer rounded to the nearest tenth is

Remember that you have to apply logarithms when the exponential equation cannot be expressed as equivalent powers.