Question

In △ABC, m∠CAB = 60° and point D ∈ BC so that AD = 10 in, and the distance from D to AB is 5in. Prove that AD is the angle bisector of ∠A.

Answer 1

Leg opposite to 30 degree converse

Explanation:

We know the inches because it is given, so we need to find the 30 degree angle using the 30 degree angle theorem. SO it would be converse.

Answer 2

Given:

In △ABC, m∠CAB = 60° and point D ∈ BC so that AD = 10 in, and the distance from D to AB is 5 in.

The distance from D to AB is 5 in.

Construction:

Take point E on AB and join ED such that ED⊥AB

Proof:

Let E be the point on AB which is 5 in from point D.

DE would be perpendicular to AB because distance is always measure in perpendicular form.

Therefore, ΔAED is a right angle triangle.

where, ∠AED=90° , AD=10 and ED=5

In ΔAED, ∠AED=90°

Using trigonometry identities

`\sin(\angle EAD)=\frac{\text{Perpendicular}}{\text{Base}}=(ED)/(AD)`

`\sin(\angle EAD)=(5)/(10)=(1)/(2)`

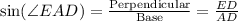
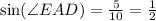
Therefore, ∠EAD=30°

But ∠CAB=60°

∠BAD=∠CAB-∠EAD=60-30 = 30°

Therefore, ∠BAD=∠EAD=30°

We can say line AD is angle bisector of ∠A. Because it divided ∠A into two equal part.

Hence Proved