Question

Suppose two initial vectors intersect at a right angle and form a resultant vector. The magnitudes of one initial vector, A, and the resultant vector, R, are given. Which formula can be used to find the magnitude of the other initial vector, B? B2 = A2 - R2 B2 = R2 + A2 B2 = A + R B2 = R2 - A2

Answer 1

The correct answer is actually D, B^2=R^2-A^2

Answer 2

The correct answer to the question will be
`B^2=\ R^2\ -\ A^2`.

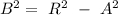Step-by-step explanation:

The two vectors are given as
`\vec A\ and\ \vec B`.

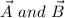As per the question, the two vectors intersect each other perpendicularly .

Hence, the angle between them is
`[\theta]=\ 90^0`

The magnitude of resultant is given as R.

From parallelogram law of vector addition, the resultant R is calculated as -

`R=√(A^2+B^2+2ABcos\theta)`

`=√(A^2+B^2+2ABcos90)`

`=√(A^2+B^2+2AB* 0)`

`=√(A^2+B^2)`

⇒
`R^2=\ A^2+B^2`

⇒
`B^2\ =\ R^2-A^2`

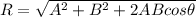
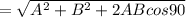
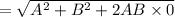
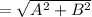
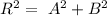
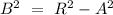
Hence, the correct relation for B will be
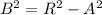`B^2=R^2-A^2`.