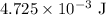Question

Calculate the energy stored in the stretched wire which will produce an extention of 0.30mm in a steel wire with a length of 4.0m and a cross sectional area of 2.0 x10^(-6) m^2 young modulus of steel is 2.1 x10^11Pa

Answer 1

Given data:

* The extension of the wire is 0.3 mm.

* The length of the wire is 4 m.

* The cross sectional area of the wire is,

`A=2.0*10^(-6)m^2`

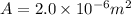
* The young modulus of the steel is,

`Y=2.1*10^(11)\text{ Pa}`

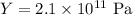
Solution:

The young modulus of the steel wire in terms of the force acting on the wire is,

`Y=(F* l)/(A* dl)`

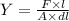
where A is the area of cross section, dl is the extension, l is the length of the wire, and F is the force acting on the wire,

Substituting the known values,

`\begin{gathered} 2.1*10^(11)^{}=(F*4)/(2.0*10^(-6)*0.3*10^(-3)) \\ 2.1*10^(11)=6.67*10^9* F \\ F=(2.1*10^(11))/(6.67*10^9) \\ F=0.315*10^2 \\ F=31.5\text{ N} \end{gathered}`

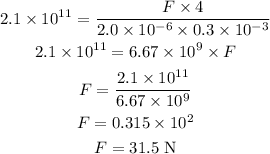
The energy stored in the stretched wire is,

`\begin{gathered} U=(1)/(2)* F* dl \\ U=(1)/(2)*31.5*0.3*10^(-3) \\ U=4.725*10^(-3)\text{ J} \end{gathered}`

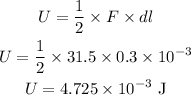
Thus, the energy stored in the stretched wire is,

`4.725*10^(-3)\text{ J}`