Question

Choose the definition for the function.D.1a. y = {-x+ 2 x<1Lx + 1--x+ 2 x > 1x = 1c. y =x < 1=&x+1b. y ={\*+{-x+ 2 xsid.y={-*+,2*21x +x < 1

Answer 1

We have two functions which are defined

Below is an image of what these functions look like without any definitions or limits.

-x+2 is the green line y x+1 is the red line

Now, if you look at the definitions, both lines start at x=1, however, their definitions are different

Let's start with the function (-x+2)

its values start at 1 and increase positively, also at the point x=1 there is no discontinuity that is to say that for this function x is greater than y equal to 1.

Now with (x+1)

its values start at 1 and decrease negatively, also at the point x=1 there is a discontinuity that means that for this function x is less than 1.

The option that accomplishes this is option d.

`\begin{gathered} (-x+2)where\Rightarrow x\ge1 \\ (x+1)where\Rightarrow x<1 \end{gathered}`

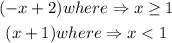
In conclusion, the answer is d option