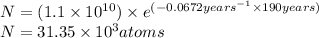Answer: Atoms of
 left in
left in
a)
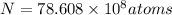
b)

c)
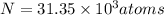
Explanation: The given reaction is a type of radioactive decay and all the radioactive decay follows first order reactions. Hence, to calculate the rate constant, we use the formula:
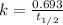
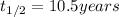
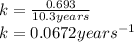
To calculate how much amount of sample is left, we use the rate law expression for first order kinetics, which is:
 ....(1)
....(1)
where,
k = rate constant =
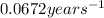
t = time taken for decay process
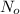 = initial amount of the reactant =
= initial amount of the reactant =

N = amount left after decay process
t = 5 years
Putting values in equation 1, we get:
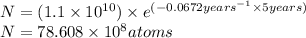
t = 30 years
Putting values in equation 1, we get:
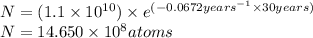
t = 190 years
Putting values in equation 1, we get: