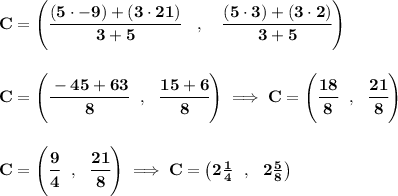Question

What are the coordinates of the point 3/5 of the way from A(-9,3) to B(21,-2)

Answer 1

so say hmmm the point C is 3/5 of the way from A to B, that means the segment AC is at a ratio of 3, whilst the segment CB is at a ratio of 5, namely 3:5, and C cuts AB to a 3:5 ratio, namely is 3/5 of the way from A to B, check the picture below. Thus,


`\bf \left. \qquad \right.\textit{internal division of a line segment} \\\\\\ A(-9,3)\qquad B(21,2)\qquad \qquad 3:5 \\\\\\ \cfrac{AC}{CB} = \cfrac{3}{5}\implies \cfrac{A}{B} = \cfrac{3}{5}\implies 5A=3B\implies 5(-9,3)=3(21,2)\\\\ -------------------------------\\\\ { C=\left(\cfrac{\textit{sum of`


`\bf C=\left(\cfrac{(5\cdot -9)+(3\cdot 21)}{3+5}\quad ,\quad \cfrac{(5\cdot 3)+(3\cdot 2)}{3+5}\right) \\\\\\ C=\left(\cfrac{-45+63}{8}~~,~~\cfrac{15+6}{8} \right)\implies C=\left( \cfrac{18}{8}~~,~~\cfrac{21}{8} \right) \\\\\\ C=\left( \cfrac{9}{4}~~,~~\cfrac{21}{8} \right)\implies C=\left(2(1)/(4)~~,~~2(5)/(8) \right)`

Answer 2

9,0

Explanation: