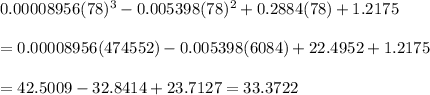The general form of a cubic model is given by:
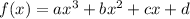
Let x represent the number of years after 1900, then from the table, we have:

Solving equations (1), (2), (3) and (4) simultaneously we get:
a = 0.00008956; b = -0.005398; c = 0.2884; d = 1.2175
Therefore, the cubic cubic model that estimates the annual consumption of cheese per person in the United States x years after 1900 is given by:
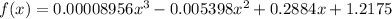
Therefore, an estimate of the annual consumption of cheese per person in the United States in 1978 (78 years after 1900) is given by: