Question

Rewrite the rational exponent as a radical by extending the properties of integer exponents. (2 points) 2 to the 3 over 4 power, all over 2 to the 1 over 2 power

A - the eighth root of 2 to the third power
B - the square root of 2 to the 3 over 4 power
C - the fourth root of 2
D - the square root of 2

Answer 1

C

Explanation:

Answer 2

C - the fourth root of 2

Explanation

First, we are going to write our expression in mathematical notation:

2 to the 3 over 4 power, all over 2 to the 1 over 2 power =
`\frac{2^{(3)/(4) }}{2^{(1)/(2) }}`

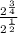
Now, we are going to use the law of exponents for division:
`(a^m)/(a^n) =a^(m-n)`

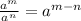
We can infer from our expression that
`a=2`,
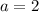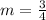`m=(3)/(4)`, and
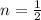`n=(1)/(2)`, so let's use our rule:

`\frac{2^{(3)/(4) }}{2^{(1)/(2) }}=2^{(3)/(4)-(1)/(2) }}=2^{(1)/(4)}`

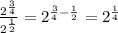
Finally, we are going to use the rule for fractional exponents:
`a^{(1)/(n) }=\sqrt[n]{a}`

Just like before, we can infer that
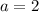`a=2` and
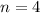`n=4`, so let's use our rule:

`2^{(1)/(4)}=\sqrt[4]{2}`

Or in words: the fourth root of 2.