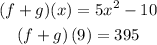
Step-by-step explanation
given
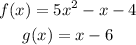
Step 1
a) (f+g) (x)
here we need to find a new function ( f+g) (x), this is the sum of the functions f and g, so to find it just add g(x) to f(x)
hence
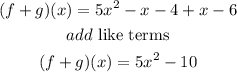
so
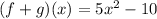
Step 2
now, we have to evaluate that function for x= 9
so
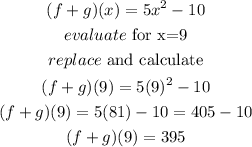
so
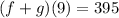
I hope this helps you