1) Let's consider both triangles ABC and ADB:
Then the proportional sides between similar triangles is:
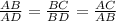
2)Since we have that AD=9.3 and BD=15.7, using the pythagorean theorem we get the following:
![\begin{gathered} AB^2=AD^2+DB^2 \\ \Rightarrow AB^2=(9.3)^2+(15.7)^2=86.5+246.5=333 \\ \Rightarrow AB=\sqrt[]{333}=18.2 \\ AB=18.2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xv2gk0z9p36f2s9xfpa7.png)
Therefore, AB=18.2 ft
3)a)the best way to represent the length from A to C is with the pythagorean theorem:
![AC=\sqrt[]{AB^2+BC^2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/rx308rkd2t1v29fxqewv.png)
b)The proportion to find the distance across the stream is the segment DC, then:

c)We can find the length by using the values for AD, BD and DB that we previously got:

Finally, we have that the length across the stream is 26.5 ft