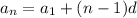
where: an - nth term, a1 - first term, and d- common difference
For the arithmetic sequence, 2, 24, 46
a1 = 2
d = 24-2 = 22
or d = 46-24 = 22 ( also 22)
for the 4th term, n =4
substituting the values in the formula
for the 4th term, n =4; a4 = 2 + ( 4 - 1 ) (22) = 2 + (3)(22) = 2 + 66 = 68
for the 5th term, n =5; a5 = 2 + ( 5 - 1 ) (22) = 2 + (4)(22) = 2 + 88 = 90
for the 6th term, n =6; a6 = 2 + ( 6 - 1 ) (22) = 2 + (5)(22) = 2 + 110 = 112
To check, 90 - 68 = 112 - 90 = 22
Answer 4th = 68, 5th = 90 and 6th = 112