Question

How many grams of C4H10 are needed to form 85 grams of carbon dioxide?

Answer 1

The mass of C4H10 needed = 28 grams

Step-by-step explanation

Given:

The mass of carbon dioxide formed = 85 grams

What to find:

The mass of C4H10 needed to form 85 grams of CO2.

Step-by-step solution:

Step 1: Write the balanced equation for the reaction.

`2C_4H_(10)+13O_2\rightarrow8CO_2+10H_2O`

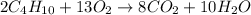
Step 2: Convert 85 grams of CO2 formed into moles.

Using the atomic masses of C and O from the periodic table; the molar mass of CO2 = 44.01 g/mol.

So, the moles of CO2 in 85 grams CO2 can be calculated using the mole formula

`\begin{gathered} Moles=\frac{Mass}{Molar\text{ }mass} \\ \\ Moles\text{ }of\text{ }CO_2=\frac{85\text{ }g}{44.01\text{ }g\text{/}mol}=1.931379232\text{ }mol \end{gathered}`

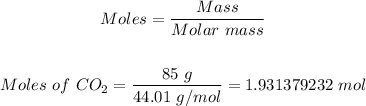
Step 3: Determine the moles of C4H10 needed.

Using the mole ratio of C4H10 to CO2 in step 1 and the moles of CO2 formed in step 2; the moles of C4H10 needed is calculated as shown below.

`\begin{gathered} 2mol\text{ }C_4H_(10)=8mol\text{ }CO_2 \\ \\ x=1.931379232mol\text{ }CO_2 \\ \\ Cross\text{ }multiply\text{ }and\text{ }divide\text{ }both\text{ }sides\text{ }by\text{ }8mol\text{ }CO_2 \\ \\ x=\frac{1.931379232mol\text{ }CO_2}{8mol\text{ }CO_2}*2mol\text{ }C_4H_(10) \\ \\ x=0.482844808\text{ }mol \end{gathered}`

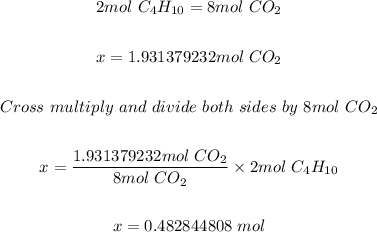
Step 4: Convert the moles of C4H10 in step 3 above to grams.

From the periodic table, the molar mass of C4H10 can be determined to be = 58.12 g/mol.

Using the same mole formula used in step 2, the mass of C4H10 is

`\begin{gathered} Mass=0.482844808mol*58.12g\text{/}mol \\ \\ Mass\text{ }of\text{ }C_4H_(10)=28.06294024\text{ }grams \\ \\ Mass\text{ }of\text{ }C_4H_(10)\approx28\text{ }grams \end{gathered}`

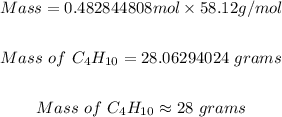
Therefore, the mass of C4H10 needed to form 85 grams of carbon dioxide is 28 grams