Question

The formula for the volume of a right cylinder is V = (pi)r^2h. Find the rate of change of the volume when r = 2 inches if dr/dt = 1/8 in./min and h = 5r. Show all your work.

Answer 1

The volume is increasing at a rate of 15π/2 squared inches per minute.

Explanation:

The formula for the volume of a right cylinder is:

`V=\pi r^2h`

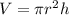
We want to find dV/dt when r = 2, dr/dt = 1/8 in/min, and h = 5r.

Since h = 5r:

`V=\pi(r)^2(5r)=5\pi r^3`

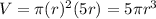
Differentiate both sides with respect to t:

`\displaystyle (dV)/(dt)=15\pi r^2(dr)/(dt)`

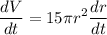
Since r = 2 and dr/dt = 1/8:

`\displaystyle (dV)/(dt)=15\pi(2)^2\Big((1)/(8)\Big)=(15\pi)/(2)`

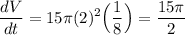
So, the volume is increasing at a rate of 15π/2 squared inches per minute.