Answer:
• The number of attendees = 1
,
• Total Cost = $744
Step-by-step explanation:
Let the number of attendees = n
A hotel in Dayton will cost $693 for a reservation, plus $51 per person.
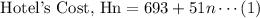
A restaurant will cost $60 per person, in addition to $684 for the reservation.
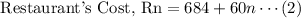
We want to find the number of attendees(n) at which the venues cost the same amount.
Equate the cost equations (1) and (2) above:
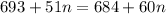
Solve the equation for n:

The number of attendees it would take for the cost to be the same amount is 1.
We determine the total cost using any of the equations:
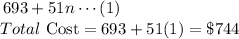
The total cost will be $744.