Answer:
The value of
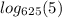 is
is
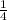
Explanation:
We want to evaluate
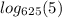 .
.
The base of this logarithm is
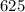 and the number is
and the number is
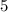 .
.
We need to express the number
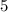 as the base
as the base
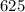 raised to a certain index.
raised to a certain index.
This implies that,
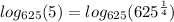
Recall now that,
 .
.
We apply this property to obtain,
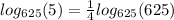
Recall again that,
 .This implies that,
.This implies that,

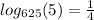
The correct answer is C.