Question

Solve this quadratic equation.
x^2 + 5x + 3 = 0

Answer 1

ALVS verified

Explanation:

x=5±√37/2

Answer 2

Hi there!
The question gives us the quadratic equation
`x^(2) +5x+3=0`, and it tells us to solve it using the quadratic formula, which goes as
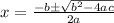
`x = (-b \pm √(b^2 - 4ac) )/(2a)`. However, we must first find the values of a, b, and c. The official quadratic equation goes as
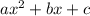
`ax^2+bx+c`, which matches the format of the given quadratic equation. Hence, the value of a would be 1, the value of b would be 5, and the value of c would be 3. Now, just plug it back into the quadratic equation and simplify to get the zeros of the equation.

`x = (-b \pm √(b^2 - 4ac) )/(2a)`

`x = (-(5) \pm √((5)^2 - 4(1)(3)) )/(2(1))`

`x = (-5 \pm √(25 - 12) )/(2)`

`x = (-5 \pm √(13) )/(2)`

`x = (-5 \pm 3.61 )/(2)`

`x = (-5 + 3.61 )/(2), x = (-5 - 3.61 )/(2)`

`x=-0.695 \ \textgreater \ \ \textgreater \ -0.7, x= -4.305 \ \textgreater \ \ \textgreater \ x=-4.31`
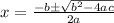
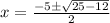
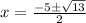
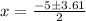
Therefore, the solutions to the quadratic equation
`x^(2) +5x+3=0` are x = -0.7 and x = -4.31. Hope this helped and have a phenomenal day!