Question

What is the most precise name for quadrilateral ABCD with verticesA(-5, 7), B(6,-3), C(10, 2), and D(-1, 12)?A. rectangleB. rhombusC. squareD. parallelogram

Answer 1

Given that

The vertices of a quadrilateral are A(-5, 7), B(6,-3), C(10, 2), and D(-1, 12).

So we have to find the type of quadrilateral ABCD.

Explanation -

First, we have to find the length of each side AB, BC, CD, and DA.

We will use the distance formula to find the length of each side

`\begin{gathered} T\text{he distance formula for point \lparen x}_1,y_1)\text{ and \lparen x}_2,y_2)\text{ is } \\ d=√((x_2-x_1)^2+(y_2-y_1)^2) \end{gathered}`

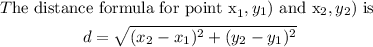
Now we will find the sides by substituting the value,

`\begin{gathered} For\text{ AB,} \\ AB=√((6-(-5))^2+(-3-7)^2) \\ \\ AB=√((6+5)^2+(-10)^2)=√(11^2+10^2)=√(121+100)=√(221) \\ \\ AB=√(221)\text{ units} \end{gathered}`
`\begin{gathered} For\text{ BC,} \\ BC=√((10-6)^2+(2-(-3))^2) \\ BC=√(4^2+(2+3)^2) \\ BC=√(16+25)=√(41) \\ BC=√(41)\text{ }units \end{gathered}`
`\begin{gathered} For\text{ CD} \\ CD=\sqrt{(-1-10)\placeholder{⬚}^2+(12-2)\placeholder{⬚}^2} \\ CD=√((-11)^2+(10)^2) \\ CD=√(121+100) \\ CD=√(221)\text{ units} \end{gathered}`
`\begin{gathered} For\text{ DA,} \\ DA=√((-1-(-5))^2+(12-7)^2) \\ DA=√((-1+5)^2+5^2) \\ DA=√(4^2+5^2)=√(16+25) \\ DA=√(41)\text{ units} \end{gathered}`

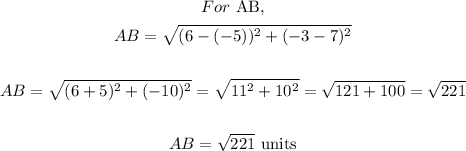
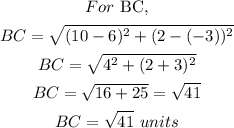
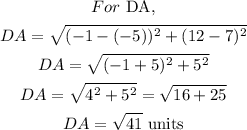
So we found that the opposite sides are equal. So it can be a parallelogram or a rectangle.

Now, we will check the triangular part ABC, by applying Pythagoras' theorem.

`\begin{gathered} In\text{ trianlge ABC, } \\ AC=√((10-(-5))^2+(2-7)^2)=√((10+5)^2+(-5)^2) \\ AC=√(15^2+5^2) \\ AC=√(225+25)=√(250) \\ Now\text{ using pythagoras theorem we have,} \\ AC^2=AB^2+BC^2 \\ √(250)^2=√(221)^2+√(41)^2 \\ 250=221+41 \\ 250\\e262 \end{gathered}`

So it is a parallelogram. Then option D is correct.

Final answer -

The final answer is a parallelogram.