Question

What are the zeroes of f(x)=(2x+3)(x-5)?

Answer 1

`-(3)/(2) , 5`

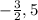
Explanation:

The zeroes of a function are the x values of the points at which the graph intersects the x-axis. All points on the x-axis have a y-value of 0, therefore, we need to find out which values of x can be plugged in to have the result be 0. This function is already factored out. So, for each expression, find which input of x makes the result equal 0.

1) So, start with 2x + 3. Set it equal to 0 and solve for x:

`2x + 3 = 0\\2x = -3\\x = -(3)/(2) \\`

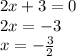
Therefore,
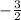`-(3)/(2)` is one of the zeroes.

2) Next, set x-5 equal to 0 and solve, too:

`x - 5 = 0 \\x = 5 \\`

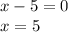
Therefore, 5 is one of the zeroes.

3) Thus, the zeroes are
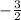`-(3)/(2)` and 5.

Answer 2

———————————————————a