Question

1. What are the coordinates of the circumcenter of a triangle with vertices A(0,1), B(2, 1) , and C(2, 5) ?

2. What are the coordinates of the centroid of a triangle with vertices A(−6, 0)

, B(−4, 4) , and C(0, 2) ?

Answer 1

your answer is a. (-6,0)

Answer 2

1.

We know that a circumcenter is the intersection of all three perpendicular bisectors of a triangle, which divides the sides equally. So, basically, we need to find a points which is equidistant from its ends of the side.

So, for points
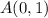`A(0,1)` and
`B(2,1)`, we have

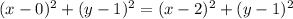`(x-0)^(2)+(y-1)^(2) =(x-2)^(2) +(y-1)^(2)`, you can observe that we just replace the coordinates in an expression which states that the distance of the two segments are equal, becuase the points
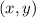`(x,y)` divdes them equally. Now, we solve the expression

`(x-0)^(2)+(y-1)^(2) =(x-2)^(2) +(y-1)^(2)\\x^(2) +y^(2) -2y+1=x^(2) -4x+4+y^(2)-2y+2\\ 1=-4x+4+2\\4x=6-1\\x=(5)/(4)`

Now, we have
`B(2,1)` and
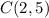`C(2,5)`, we do the same process

`(x-2)^(2) +(y-1)^(2) =(x-2)^(2) +(y-5)^(2) \\(y-1)^(2) =(y-5)^(2)\\y^(2)-2y+1=y^(2) -10y+25\\ -2y+10y=25-1\\8y=24\\y=3`

Therefore, the circumcenter is at
`((5)/(4),3)`

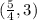
2.

The centroid of a triangle is defined as

`C_(x)=(A_(x)+B_(x) +C_(x) )/(3)\\ C_(y)=(A_(y)+B_(y) +C_(y) )/(3)`

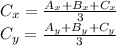
Where

`A_(x)=-6; A_(y)=0\\B_(x)=-4; B_(y)=4\\C_(x)=0; C_(y)=2`

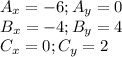
Replacing all values, we have

`C_(x)=(A_(x)+B_(x) +C_(x) )/(3)=(-6-4+0)/(3)=-(10)/(3) \\ \\C_(y)=(A_(y)+B_(y) +C_(y) )/(3)=(0+4+2)/(3)=(6)/(3)=2`

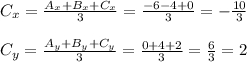
Therefore, the centroid is at
`C(-(10)/(3) ;2)`