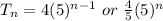Question

What is the explicit rule for this geometric sequence? 4,45,425,4125,…

Answer 1

The Answer Is An=4⋅(1/5)n−1

Explanation:

Answer 2

You did not write the question correctly but I will try to answer the question according to 2 possible interpretations of your question.

Case 1:

Given the geometric sequence:


`4,\ (4)/(5) ,\ (4)/(25) ,\ (4)/(125) ,\ .\ .\ .`

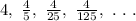
Common ratio is given by
`r= (2nd\ term)/(1st\ term) = ( (4)/(5) )/(4) = (1)/(5)`

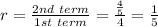
The explicit rule of a geometric sequence is given by
`T_n=ar^(n-1)`

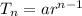
Therefore, the explicit rule of the given sequence is
`T_n=4\left( (1)/(5) \right)^(n-1)\ or\ 20\left( (1)/(5) \right)^n`


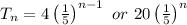
Case 2:

Given the geometric sequence:


`4,\ 4\cdot5,\ 4\cdot25,\ 4\cdot125,\ .\ .\ .`

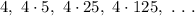
Common ratio is given by
`r= (2nd\ term)/(1st\ term) = (4\cdot5)/(4) = 5`

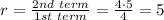
The explicit rule of a geometric sequence is given by
`T_n=ar^(n-1)`

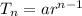
Therefore, the explicit rule of the given sequence is
`T_n=4(5)^(n-1)\ or\ (4)/(5)(5)^n`